Timo Reisner plant Experimente mit einer Miniaturversion des Darmstädter Versuchsstands.

Das Verhalten von Fluid-Granulat-Mischungen kann zum Beispiel mit Glaskugeln untersucht werden.

Versuche mit Wasser und Glaskugeln, die aus einem Mini-Behälter fließen, sollen in Zukunft helfen, die theoretischen Daten im Experiment zu überprüfen.

1/3

Umwelt Wenn der Boden ins Fließen gerät

Erdrutsche, Schuttströme und Schlammlawinen vergraben jährlich hunderte Menschen unter sich. Was physikalisch passiert, wenn der Boden sich bewegt, untersuchen Wissenschaftler an der RUB.

In der Natur sind geophysikalische Massenströme so komplex, dass sie sich messtechnisch kaum erfassen lassen. Am Lehrstuhl für Kontinuumsmechanik beschäftigen wir uns daher theoretisch mit diesen Fließprozessen. Wir betrachten Mischungen aus Körnern und Flüssigkeiten unter klar definierten und kontrollierbaren Bedingungen, zum Beispiel wie ein Kies-Wasser-Gemisch aus einem drei Meter hohen Behälter fließt. Wir arbeiten dabei eng mit Geotechnikern der Technischen Universität Darmstadt zusammen, die ebendiesen Fließprozess experimentell untersuchen.

Kies und Wasser setzen sich in Bewegung

Bei den Versuchen der Darmstädter Kollegen öffnet sich zu Beginn am unteren Ende des gefüllten Behälters eine Klappe. Mit Wucht setzt sich das Kies-Wasser-Gemisch in Bewegung und strömt innerhalb von zehn Sekunden aus. Moderne Messtechnik zeichnet die Vorgänge im Inneren auf.

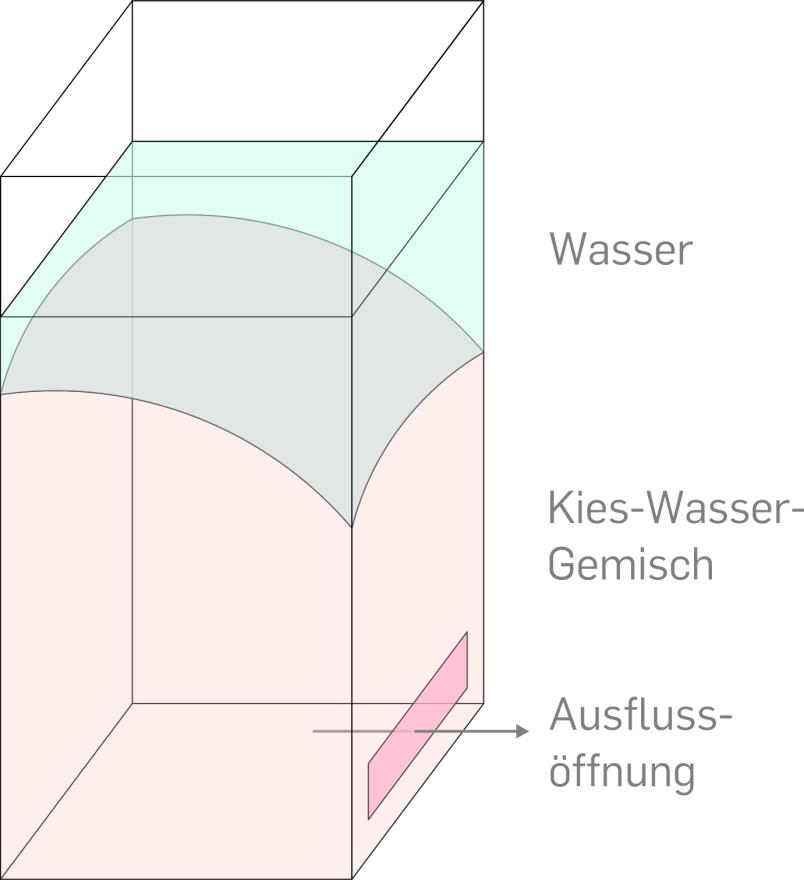
Skizze des Darmstädter Versuchstands

Prozesse wie in dem Versuchsstand beschreiben wir in der Kontinuumsmechanik mit mathematischen Modellen. Diese helfen zum einen, die physikalischen Gesetzmäßigkeiten natürlicher Prozesse besser zu verstehen; zum anderen kann man mit ihnen voraussagen, wie sich ein System bei veränderten Bedingungen verhält, zum Beispiel wenn wir die Größe der Klappe ändern oder die Korngröße des verwendeten Kieses. Ein solches Modell entwickeln wir gemeinsam mit Mathematikern der Technischen Universität Bukarest, Rumänien.

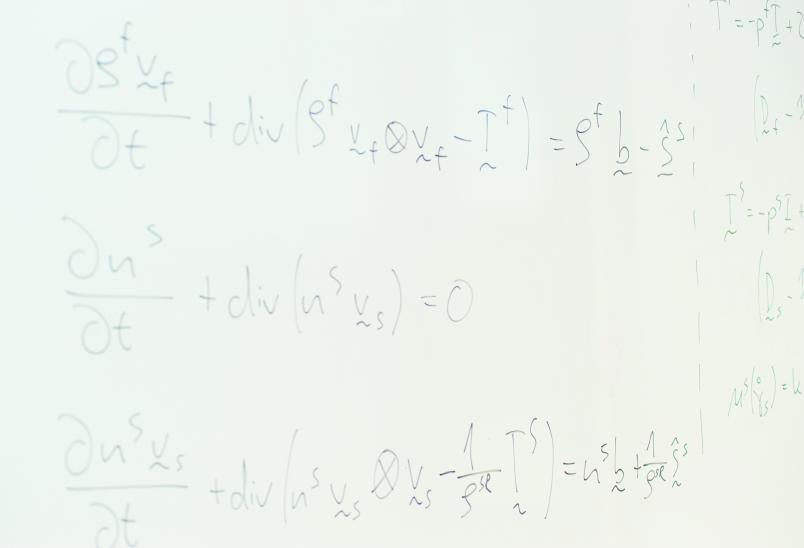
Komplexe Gleichungen sind notwendig, um das Fließverhalten von Fluid-Granulat-Mischungen mathematisch zu beschreiben.

Ziel ist es, den im Darmstädter Labor beobachteten Strömungsprozess so genau wie möglich nachzubilden und somit die Fließbewegungen bei Massenströmen zu begreifen. Wir simulieren, wie schnell Flüssigkeit und Granulat aus dem Behälter fließen, welche Anteile sie an dem Gemisch haben und welche Drücke an unterschiedlichen Stellen im Behälter herrschen. Die Ergebnisse sollten den experimentell bestimmten Werten entsprechen. Bei der Modellentwicklung stützen wir uns auf die Mischungstheorie.

Kontinuumsmechanik und Mischungstheorie

Die Materie, die uns umgibt, ist aus kleinsten Bestandteilen zusammengesetzt: Eine Zeitschrift zum Beispiel besteht aus einzelnen Molekülen von Papier und Druckerfarbe, welche wiederum aus einzelnen Atomen zusammengesetzt sind. Um das mechanische Verhalten des Heftes zu beschreiben, könnten wir also jedes einzelne Molekül und seine Wechselwirkung mit allen anderen Molekülen beschreiben – ein zweifellos extrem aufwendiges Unterfangen.

In der Kontinuumsmechanik nehmen wir daher vereinfachend an, dass die Materie in einem Körper gleichmäßig (kontinuierlich) verteilt ist und den Körper vollständig ausfüllt. Betrachten wir also einen kleinen Ausschnitt des Körpers, so sehen wir keine einzelnen Moleküle mehr. Wir kennen aber die durchschnittlichen Eigenschaften der Moleküle in dem Ausschnitt. Solange der betrachtete Körper groß genug ist und ausreichend viele einzelne Bestandteile enthält, führt dieser Ansatz zu sehr guten Ergebnissen.

Die Mischungstheorie ist in gewisser Weise eine Erweiterung dieses Kontinuumsansatzes: Sie besagt, dass wir auch bei makroskopisch unterscheidbaren Bestandteilen einer Mischung, wie hier den einzelnen Kieskörnern und Wasser, dasselbe Konzept verwenden dürfen – solange wir keine einzelnen Körner betrachten, sondern über eine Vielzahl von Körnern mitteln. Bei dieser Betrachtungsweise geht also die Information über das einzelne Korn verloren. Wir wissen aber, wie die Mischung an jedem Punkt im Raum prozentual zusammengesetzt ist und wie sich die Bestandteile im Mittel verhalten.

Mathematisch gesehen ist es zunächst egal, um was für eine Flüssigkeit und um welche Art von Körnern es sich handelt, ob wir es also zum Beispiel mit Kies, Sand oder Glaskugeln zu tun haben. Wir sprechen daher verallgemeinernd von einer Granulat-Fluid-Mischung. Für eine solche Mischung leiten wir zunächst ganz allgemeine Gleichungen her, die auf physikalischen Grundprinzipien beruhen.

Wir sprechen von Erhaltungsgleichungen, weil sie ausdrücken, dass zum Beispiel die Masse innerhalb eines geschlossenen Systems – wie einem luftdichten Raum – nicht kleiner oder größer werden kann. Damit wir jedoch die Gleichungen überhaupt lösen können, benötigen wir im nächsten Schritt Informationen darüber, wie sich die verwendeten Materialien im Versuch konkret verhalten.

Gedankenexperiment zum Verhalten von Wasser

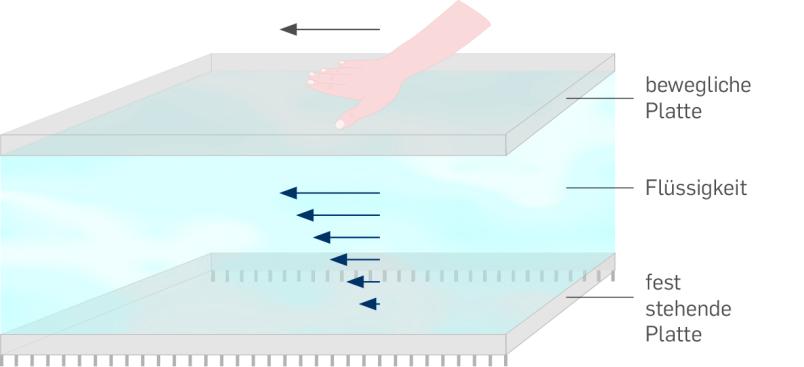
Das Materialverhalten von Wasser können wir uns beispielsweise mit folgendem Gedankenexperiment vorstellen: Wir füllen den Raum zwischen zwei unendlichen parallelen Glasplatten mit Wasser. Die untere Platte halten wir fest. Die obere schieben wir in eine Richtung, wobei der Abstand zwischen beiden Platten gleich bleibt. Aufgrund der Reibung im Innern der Wasserschicht bewegt sich die obere Glasplatte nun mit konstanter Geschwindigkeit, und die Wasserschicht wird entsprechend verformt.

Flüssigkeiten können Widerstand leisten

Schieben wir nun die obere Glasplatte etwas kräftiger an, so bewegt sie sich schneller. Die Kraft, mit der wir die Platte anschieben, und die Geschwindigkeiten innerhalb der Wasserschicht sind in diesem Beispiel linear voneinander abhängig. Man bezeichnet ein solches Verhalten von Flüssigkeiten als Newtonsche Rheologie.

Wie viel Widerstand ein Newtonsches Fluid seiner Verformung entgegensetzt, wird durch seine Zähflüssigkeit bestimmt: je dickflüssiger, desto höher der Widerstand, gegen den die Glasplatte bewegt werden muss. Dieses Materialverhalten beschreiben wir mathematisch mit einer sogenannten Konstitutivbeziehung, die dann einen Teil unseres Modells bildet.

Gedankenexperiment zum Materialverhalten von Wasser. Die beiden Glasplatten sind in der Vorstellung unendlich groß – sonst würde das Wasser an den Seiten herausfließen.

Nun müssen wir uns über das Materialverhalten der Körner Gedanken machen. Dazu ersetzen wir das Wasser in unserem Gedankenexperiment durch ein Granulat, also Sand, Kies oder Glaskugeln. Schieben wir die obere Glasplatte nur leicht an, so verhält sich der Kornverband wie ein Festkörper – die Glasplatte rührt sich nicht von der Stelle. Die Zähflüssigkeit ist gewissermaßen unendlich groß. Bei Erreichen einer bestimmten Kraft kommt das Granulat aber ebenfalls ins Fließen, und die obere Glasplatte bewegt sich.

Festkörper können sich wie Flüssigkeiten verhalten

Anstatt wie ein Festkörper verhält sich das Material auf einmal wie eine Flüssigkeit, vergleichbar mit dem Sand einer Sanduhr, die gerade umgedreht wird. Erhöhen wir nun wieder die Kraft, mit der wir die Glasplatte anschieben, so ändern sich auch die Geschwindigkeiten innerhalb der Granulatschicht – der Zusammenhang ist aber nicht linear wie bei einem Newtonschen Fluid. Auch dieses komplexe Materialverhalten beschreiben wir in unserem Modell mit einer Konstitutivbeziehung.

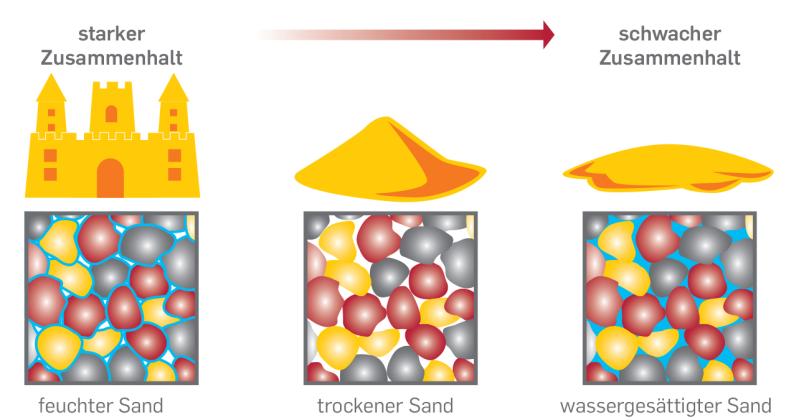
Weiterhin müssen wir Antworten auf die folgenden Fragen in unsere Konstitutivgleichungen einbauen: Welchen Beitrag leistet die Flüssigkeit im Porenraum als „Schmierstoff“ zum Fließverhalten des Granulats? Welche Auswirkungen hat die Korngröße? Je größer die Körner, desto geringer ist der Einfluss der Kohäsion, also des inneren Zusammenhalts des Kornverbandes – aus feuchtem Kies kann man keine Sandburg bauen. Welchen Einfluss hat die Form der einzelnen Körner? Eckige Kieskörner fließen schlechter als perfekt runde Glaskugeln.

Der Wassergehalt beeinflusst die Materialeigenschaften eines Kornverbandes von Sandkörnern: Feuchter Sand verhält sich wie ein Festkörper. Trockener Sand kann Eigenschaften eines Festkörpers oder einer Flüssigkeit annehmen. Bei vollständig wassergefüllten Poren zwischen den Körnern ergibt sich eine fließfähige Mischung.

Werte wie die minimal erforderliche Kraft, um die Glasplatte in unserem Gedankenexperiment zu bewegen, oder die Zähflüssigkeit eines wassergesättigten Granulats lassen sich kaum im Labor bestimmen. Daher treffen wir zunächst plausible Annahmen, bestimmen dann aus unserem Gleichungssystem Lösungen und vergleichen diese mit den experimentellen Ergebnissen.

Weichen unsere Lösungen von den experimentellen Werten ab, so passen wir die Konstitutivgleichungen, die das Materialverhalten beschreiben, entsprechend an. In der Wahl dieser Konstitutivgesetze liegt also das Ziel unserer Forschung: Wir wollen sie so anpassen, dass sie das reale Fließverhalten von Fluid-Granulat-Mischungen wiedergeben, und auf diese Art das Materialverhalten der Mischung verstehen.

Komplizierte Gleichungen

Bevor es soweit ist, müssen wir aber noch eine weitere Hürde nehmen: Die Gleichungen sind so kompliziert, dass sie sich nicht einfach mit Zettel und Stift lösen lassen – stattdessen benötigen wir eine numerische Methode, also ein leistungsfähiges Rechenverfahren, mit dem sich Lösungen näherungsweise am PC bestimmen lassen.

Da es keine Software gibt, in die sich unser Gleichungssystem implementieren lässt, müssen wir diese erst entwickeln – ein zeitaufwendiges Unterfangen. Mit unserem Modell und der entsprechenden Software haben wir bereits einfachere Prozesse wie die Sedimentation, also das Absinken eines Granulats unter Schwerkrafteinfluss, simuliert.

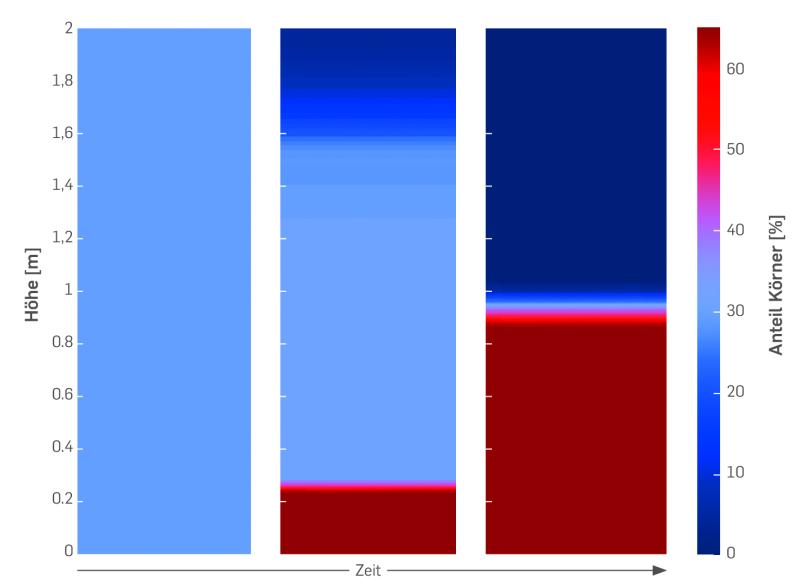
Simulation der Sedimentation eines Granulats. Links ist das Granulat noch gleichmäßig verteilt, im mittleren Bild hat sich bereits ein Teil abgesetzt. Oben bildet sich ein Klarwasserbereich. Rechts ist das Granulat vollständig sedimentiert.

Dabei haben wir nur eine Raumdimension betrachtet, denn die Körner bewegen sich nur in eine Richtung: nach unten. Die Simulationsergebnisse sind den Ergebnissen experimenteller Sedimentationstests qualitativ sehr ähnlich. Das zeigt, dass unser Modell und die Rechenmethode prinzipiell funktionieren. Sie sagen zum Beispiel scharfe Grenzflächen voraus, etwa zwischen vollständig sedimentiertem Granulat und Klarwasserbereich. Die meisten numerischen Methoden haben Schwierigkeiten mit solchen plötzlichen Übergängen.

Nachdem die ersten Tests positiv verlaufen sind, kann nun das Programm in eine andere Programmiersprache übersetzt werden, um es auch auf hochleistungsfähigen Rechnern mit vielen Prozessoren lauffähig zu machen und Simulationen in zwei oder drei Dimensionen zu ermöglichen. Das bringt uns wieder einen Schritt näher an die richtigen Konstitutivbeziehungen und somit an die Gesetzmäßigkeiten, die Schuttströmungen zugrunde liegen.