Topologie Claudius Zibrowius verknotet die Mathematik
Der neu ernannte Professor in der Topologie befasst sich mit der Beschreibung von mathematischen Knoten. Seinem Büro kann man das auf den ersten Blick ansehen.
Obwohl Claudius Zibrowius erst seit ein paar Wochen an der Ruhr-Universität Bochum ist, ist sein Büro bereits total verknotet. Auf den Tischen liegen verknotete Seile in allen Farben des Regenbogens, manche von ihnen stecken anteilig in durchsichtigen Plexiglaskugeln. Daneben eine Kaffeetasse, auf der zig verschiedene Knoten abgebildet sind – ein Geschenk zur Promotion, das passender nicht hätte sein können. Denn die Knoten haben es Zibrowius einfach angetan. Seit er in seinem Masterstudium einen wissenschaftlichen Artikel des berühmten Mathematikers Dror Bar-Natan zu diesem Thema las, ließ es ihn nicht mehr los. „Das Paper ist einer der Gründe, warum ich heute noch Mathe mache“, sagt er. Seit April 2024 tut er das als Professor für Niedrigdimensionale Topologie an der Fakultät für Mathematik.
Die ganze Mathematik ist eigentlich eine einzige Klassifizierungsmaschinerie.
Claudius Zibrowius
„Es gibt unendlich viele Knoten“, erklärt Claudius Zibrowius. „Unser Ziel ist es, sie zu klassifizieren. Die ganze Mathematik ist eigentlich eine einzige Klassifizierungsmaschinerie.“ Mathematisch herauszufinden, welche Knoten Gemeinsamkeiten haben und in dieselbe Klasse von Objekten gehören, ist kompliziert. „Wir überprüfen im Grunde, ob sich ein Knoten in einen anderen umwandeln lässt“, sagt der Forscher. Das ist so, als würde man mehrere Knoten in ein Seil machen, die Enden des Seils miteinander verbinden und dann schauen, ob man das Gebilde so verformen kann, dass daraus ein bestimmter anderer Knoten wird. Mathematisch helfen bei diesem Prozess die sogenannten Invarianten – sozusagen unveränderbare Eigenschaften, wie die Anzahl der Löcher in dem Knotengebilde.
Keine Formeln, sondern bunte Bilder
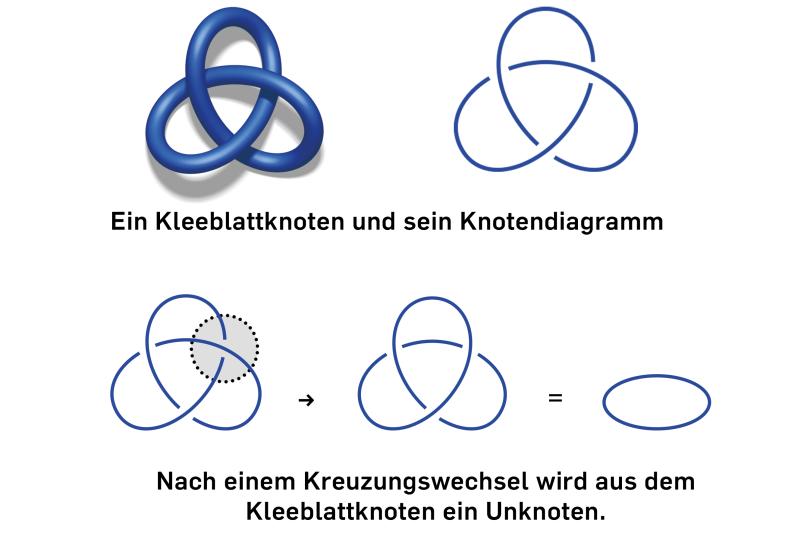
Gleichungen helfen dabei oft nicht weiter. „Es ist kompliziert, einen Knoten in eine Formel zu fassen“, so Zibrowius. Stattdessen projiziert er den Knoten auf eine zweidimensionale Ebene und arbeitet mit dem so entstehenden Bild. „Wir stellen uns den Schatten vor, den ein Knoten auf eine Oberfläche werfen würde“, beschreibt er, und demonstriert das anhand eines der verknoteten Seile in seinem Büro. „An den Stellen, an denen sich die Seile kreuzen, müssen wir zusätzlich vermerken, welcher Strang oben liegt und welcher unten“, ergänzt er. So entsteht ein Knotendiagramm, die Basis für seine Arbeit.
Anschaulich wird das eigentlich abstrakte Thema anhand der vielen Seile in seinem Büro, mit denen er die mathematischen Operationen, die er vornimmt, visualisieren kann. Übrigens handelt es sich bei diesen Knotenmodellen nicht um Artikel von der Stange. „Das war ein Corona-Projekt“, erzählt der Forscher lachend. Er kaufte verschiedene Seile, schnitt sie in unterschiedliche Längen und versah sie mit Magneten, um die Enden leicht verbinden zu können. Manche davon steckte er in Plexiglaskugeln, um zu zeigen, wie man Knoten lokal untersuchen kann, indem man sich auf nur bestimmte verknotete Teile eines Knoten fokussiert. So wird mathematische Grundlagenforschung anfassbar.
ERC-Projekt
Von der Relevanz dieser Arbeit hat Zibrowius auch den Europäischen Forschungsrat ERC überzeugen können. Insgesamt 1,4 Millionen Euro Fördermittel bekommt er zwischen 2024 und 2029 aus einem Starting Grant für die Erforschung von Knoten. Allerdings klappte es mit seinem Antrag erst im zweiten Anlauf. „Um Drittmittel zu bekommen, gehört auch Glück dazu“, weiß er und schaut durchaus kritisch auf das System der Drittmitteleinwerbung. „Wenn ich sehe, wie viel Zeit von der Antragstellung und Begutachtung aufgefressen wird, frage ich mich manchmal, ob das sinnvoll ist. Zwar habe ich auch keine Patentlösung, wie man es besser machen könnte“, gibt er zu, „aber ein guter Anfang wäre, mehr permanente Stellen im akademischen Mittelbau zu schaffen.“ Zibrowius freut sich jedenfalls, dank der ERC-Förderung fünf Jahre lang wenig Zeit in das Schreiben von Anträgen investieren zu müssen und somit mehr Zeit zu haben, um den ein oder anderen mathematischen Knoten zu lösen.
Mehr zum ERC Grant
Knoten sind mathematisch interessante Objekte. Wie man sie klassifizieren kann und wie man unterschiedliche Knoten ineinander umwandeln kann, sind Fragen der topologischen Forschung. Darum geht es im weitesten Sinne auch im ERC-Grant „Cut-and-paste conjectures and multicurves”, kurz CAPCAM, von Claudius Zibrowius.
Ein Knoten besteht aus einem Stück Seil, dessen Enden miteinander verklebt sind. Mathematisch modelliert man solche Objekte als sogenannte Einbettungen vom Kreis in den drei-dimensionalen reellen Raum. Da sich Knoten nur umständlich mit Formeln beschreiben lassen, nutzen Mathematikerinnen und Mathematiker sogenannte Knotendiagramme. Dafür projizieren sie Knoten auf eine zweidimensionale Fläche – so, als würde man den Schatten abzeichnen, den ein verknotetes Seil auf ein Blatt wirft. An den Punkten, an denen sich zwei Seilstränge kreuzen, wird im Diagramm vermerkt, welcher Strang oben und welcher unten verläuft. Wenn man an einem solchen Punkt die Stränge vertauscht, also quasi einen Strang durch den anderen hindurchschiebt, ändert sich im Allgemeinen der Knoten, der durch das Diagramm beschrieben wird. Dadurch kann auch ein völlig unverknotetes Objekt, der sogenannte Unknoten, entstehen.
Um Knoten miteinander vergleichen zu können, suchen die Forschenden nach Invarianten, also nach Eigenschaften, die unverändert bleiben, wenn man einen Knoten verformt. Zum Beispiel hat der Unknoten die Eigenschaft, dass er eine Kreisscheibe berandet; der Kleeblattknoten hat diese Eigenschaft nicht. Der Kleeblattknoten lässt sich daher nicht in den Unknoten verformen. Die beiden Knoten sind grundlegend verschieden.
In seinem Forschungsprojekt befasst sich Claudius Zibrowius unter anderem mit der sogenannten kosmetischen Kreuzungsvermutung. Einfach ausgedrückt besagt die Vermutung, dass ein Kreuzungswechsel einen Knoten nur dann nicht grundlegend verändert, wenn er es offensichtlich nicht tut. Der mathematische Beweis dafür steht aber noch aus. Mit seinem ERC-Projekt möchte Claudius Zibrowius dazu beitragen, daran etwas zu ändern.
Der Starting Grant ist mit 1,4 Millionen Euro dotiert. Das Projekt startet 2024.
