Gesammelte Patientenakten auszuwerten, ohne die Privatsphäre zu verletzen, ist nicht leicht.
RUB-Mathematiker entwickeln Techniken zum Verrauschen von Daten, die die Privatsphäre bei der Analyse schützen sollen.
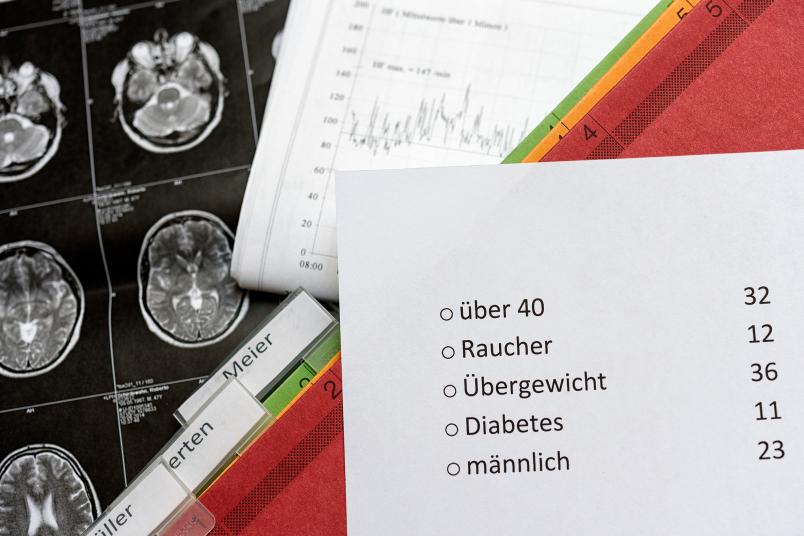
Analyse gesammelter Daten Wie Mathematik Patienten schützt
Patientenakten könnten Hinweise enthalten, wie man Krankheiten frühzeitig erkennen kann. Doch wie kann man die gesammelten Daten auswerten, ohne die Privatsphäre der Patienten zu verletzen? Hier hilft Mathematik.
Selbstständig lernende Computerprogramme können große Datenmengen durchforsten und Regelmäßigkeiten aufspüren. Solche Programme kommen zum Beispiel in modernen Spam-Filtern zum Einsatz: Sie beobachten, welche E-Mails die Benutzer als Spam markieren, und lernen daraus, was Spam-E-Mails ausmacht, ohne dass man ihnen explizit vorgibt, woran sie das erkennen können.
Zusammenhänge in gesammelten Patientendaten aufspüren
Dieses maschinelle Lernen hilft nicht nur, Spam-Filter zu verbessern, sondern generell dort, wo große Datenbestände auf Muster untersucht werden sollen, etwa bei Suchmaschinen, bei automatischer Spracherkennung oder auch bei der Analyse medizinischer Daten. Hier könnten Algorithmen in einem Stapel von Patientenakten Zusammenhänge erkennen und beispielsweise Kriterien finden, Krankheiten frühzeitig zu diagnostizieren.
„Dabei muss jedoch sichergestellt werden, dass die Privatsphäre einzelner Patienten geschützt ist“, warnt Prof. Dr. Hans Simon vom Lehrstuhl Mathematik und Informatik. Er beschäftigt sich zusammen mit den Doktoranden Francesco Alda und Filipp Valovich mit der Frage, wie empfindliche Daten statistisch ausgewertet werden können, ohne die Anonymität der beteiligten Personen preiszugeben.
Speziell untersuchen die Mathematiker eine Form des maschinellen Lernens, die auf sogenannte Zählanfragen eingeschränkt ist. Das funktioniert wie folgt: Wenn ein Algorithmus zum Beispiel eine Patientendatenbank auswerten soll, ist es ihm nur gestattet, Ja/Nein-Fragen zu stellen und zu zählen, bei wie vielen Patienten die Antwort „Ja“ lautet.
Erlaubte Fragen sind zum Beispiel: Ist die Person Raucher? Ist die Person männlich? Wiegt die Person mehr als 80 Kilogramm? Schickt ein Lern-Algorithmus diese Fragen an eine Patientendatenbank, erhält er als Antwort drei Zahlen: die Anzahl der Raucher, die Anzahl der Männer und die Anzahl der Patienten, die schwerer als 80 Kilogramm sind.
Daten verrauschen
Das Prinzip der Zählanfragen klingt anonym – schließlich ist das Resultat bloß eine statistische Zusammenfassung. Trotzdem ist es möglich, Informationen über einzelne Patienten zu gewinnen. Hans Simon und seine Mitarbeiter untersuchen deshalb Mechanismen wie „Randomized Response Schemes“, die die Privatsphäre der Patienten schützen sollen.
Dabei werden die Patientendaten verrauscht, das heißt, sie werden zufällig verändert. Vereinfacht gesprochen ist es so, als würde bei jedem Patienten gewürfelt und die Augenzahl auf die Werte in der Akte aufaddiert. Das Verfahren verändert die einzelnen Patientendaten heftig und unvorhersehbar, macht sich im Idealfall bei statistischen Zusammenfassungen jedoch nicht stärker bemerkbar als eine ohnehin in den Daten vorhandene statistische Zufallsschwankung.
Was bedeutet anonym?
Um dem Idealfall nahe zu kommen, muss das Verrauschen bestimmte Rahmenbedingungen erfüllen. „Unsere Herausforderung ist es, solche Rahmenbedingungen zu finden und klar zu formulieren“, erklärt Hans Simon. „Wir suchen also Bedingungen für das zufällige Verrauschen, die einerseits dafür sorgen, dass die einzelnen Daten so stark verändert werden, dass die Patienten nicht mehr identifiziert werden können, andererseits aber garantieren, dass der veränderte Datenbestand trotzdem ähnliche Antworten an den Lern-Algorithmus zurückliefert wie der ursprüngliche Datenbestand.“
Das ist in einem Satz schnell beschrieben, bedeutet in der Praxis für Mathematiker aber eine kleinteilige, komplexe Gedankenarbeit. Zuerst müssen sie genau definieren, was die Begriffe bedeuten, um die es geht: Was soll es exakt heißen, dass Patienten „anonym“ bleiben? Was soll es exakt heißen, dass die Antworten an den Lern-Algorithmus „ähnlich“ sind?
Anschließend suchen sie nach Bedingungen, aus denen sich herleiten lässt, dass das Verrauschen die Patientendaten anonymisiert, aber statistische Zusammenfassungen nicht substanziell verfälscht.
Einzelne Patienten in einer Datenbank wiederfinden
Die Mathematiker um Hans Simon beschäftigen sich bei ihrer Suche mit „Differential Privacy“. Das Konzept geht auf die US-amerikanische Informatikerin Cynthia Dwork zurück und gibt Antwort auf die Frage, was Anonymität streng mathematisch bedeuten kann: Differential Privacy ist ein Maß dafür, wie gut ein einzelner Patient in einer Datenbank identifiziert werden kann.
Dazu nimmt man an, man hat eine konkrete Zählanfrage und zwei Datenbanken A und B, die sich nur in einem einzigen Patienten unterscheiden. Das zufällige Verrauschen erfüllt Differential Privacy, wenn es so gut wie egal ist, ob die Datenbank A oder die Datenbank B gefragt wurde; das heißt, wenn die Wahrscheinlichkeit für eine bestimmte Sammelantwort auf die Zählfrage in beiden Fällen ähnlich ist.
„Das Gesamtergebnis der Anfrage hängt also nicht so stark von einem einzelnen Patienten ab“, erläutert Hans Simon. Ebenso nutzen er und seine Kollegen exakte Definitionen, um mathematisch genau festzulegen, was es heißt, dass aus den verrauschten Daten ähnliche statistische Schlüsse gezogen werden können wie aus den Originaldaten; man spricht hier von Accuracy.
Daten als Vektoren darstellen
Hans Simons Team möchte beim Verrauschen der Daten beide Anforderungen erfüllen, das heißt sowohl Differential Privacy als auch Accuracy gewährleisten. Dafür haben die Forscher einen Trick angewandt: Sie haben einen Zusammenhang zu einem anderen Thema in der Mathematik erkannt, zu sogenannten linearen Arrangements. Dorthin haben sie das Problem übersetzt.
Die Wissenschaftler stellen sowohl jede einzelne Patientenakte als auch jede erlaubte Zählanfrage als einen Vektor dar, das heißt als einen Pfeil in einem geometrischen Raum. Eine Ja-Antwort liegt vor, wenn die Pfeile von Patientenakte und Zählanfrage einen spitzen Winkel bilden. Eine Nein-Antwort liegt vor, wenn die Pfeile einen stumpfen Winkel bilden.
Vektoren statt Originaldaten verrauschen
Nun wird das Verrauschen nicht mehr auf den ursprünglichen Patientendaten ausgeführt, sondern auf den ihnen zugeordneten Pfeilen. Hans Simon und sein Team haben bewiesen, dass das Verrauschen mit diesem Verfahren gut funktioniert, das heißt sowohl Differential Privacy als auch Accuracy erfüllt. Die Voraussetzung ist, dass die spitzen Winkel wirklich spitz sind, das heißt deutlich kleiner als 90 Grad, und die stumpfen Winkel wirklich stumpf, also deutlich größer als 90 Grad.
Die Bochumer Mathematiker haben ein erstes Zwischenziel erreicht, wollen ihre Forschungsergebnisse aber noch erweitern. „Das Übersetzen der Patientendaten und Algorithmus-Anfragen in den geometrischen Raum ist eine große Hürde“, bedauert Hans Simon. „Es gibt kein allgemeines Rezept, wie man das anstellen kann. Zudem gibt es Typen von Datenbankanfragen, von denen man weiß, dass sie nicht geeignet geometrisch dargestellt werden können.“
Es wäre großartig, wenn sich reale Daten durch synthetische Daten ersetzen ließen.
Hans Simon hat eine Vision, die auf eine Idee des US-amerikanischen Forschers Avrim Blum zurückgeht: „Es wäre großartig, wenn sich reale Daten durch synthetische Daten ersetzen ließen, aus denen man keine Informationen mehr über die Patienten gewinnen, aber die gleichen statistischen Schlüsse ziehen kann.“ Man könnte solche synthetischen Daten dann unbeschränkt für die Allgemeinheit zugänglich machen. „Aus vorliegenden Ergebnissen der Forschergemeinde weiß man, dass sich dieses Idealziel nicht erreichen lassen wird“, sagt Hans Simon. Es könnte aber eine Triebfeder sein, die weitere wichtige Ergebnisse im Spannungsfeld zwischen statistischer Datenanalyse und Privatheit hervorbringt.
