Standpunkt
Künstliche Intelligenz forschen lassen?
In der Mathematik haben Algorithmen Zusammenhänge entdeckt, die Expertinnen und Experten zuvor verborgen geblieben waren. Kein Grund, die Füße hochzulegen und mit der Forschung aufzuhören, meint Christian Stump.
Der Einsatz von Techniken des maschinellen Lernens und der Künstlichen Intelligenz (KI) verändert nicht nur die Arbeitswelt in der Industrie, sondern ebenfalls den Forschungsalltag. Die mathematische Grundlagenforschung kommt einem dabei vielleicht nicht als erstes als Anwendungsgebiet in den Sinn. Und tatsächlich sind die mit KI verbundenen Veränderungen der Forschungswelt bisher weitestgehend an der Mathematik vorbeigegangen.
Ich denke aber, das wird nicht so bleiben.
Auch wenn dieser Ansatz noch nicht etabliert ist, werden KI-Methoden bereits erfolgreich in der mathematischen Grundlagenforschung angewandt. Zum einen suchen Mathematikerinnen und Mathematiker eigentlich immer nach guten Beispielen für ihre Theorien. Wenn ich eine Theorie für Objekte im dreidimensionalen Raum entwickle, sollte ich diese zumindest einmal an den Platonischen Körpern testen; das sind fünf Körper, zu denen beispielsweise Würfel oder Tetraeder gehören. Mit dem Computer könnte man unzählige Beispiele generieren und jedem Beispiel einen „Wie-gut-ist-dieses-Beispiel-für-mich-geeignet“-Wert zuweisen. Dieser Wert liefert dann einen perfekten Ansatz für Methoden der KI, um aus den generierten Beispielen die für mich interessanten herauszufiltern. Das kann eine KI vielleicht sogar besser als ich.
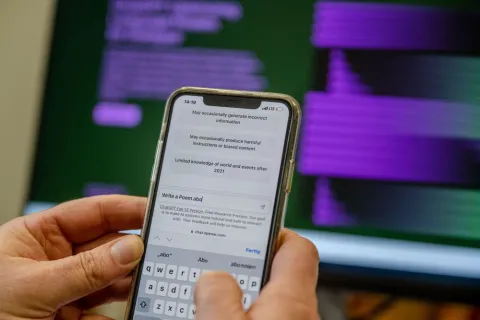
Zum anderen, und das ist etwas subtiler, gibt es erste Situationen, in denen KI im Kern der Forschung genutzt wurde, der eigentlich erst durch menschliche Intuition und Kreativität möglich wird. Im Jahr 2021 in der Zeitschrift Nature veröffentlichte Ergebnisse in dieser Richtung haben Mathematikerinnen und Mathematiker weltweit aufhorchen lassen. Darin wurden wichtige und kreative Fortschritte in seit vielen Jahren offenen Forschungsfragen erzielt. Die KI hat Zusammenhänge erkannt, die Expertinnen und Experten zuvor noch nicht gefunden hatten.

Eine KI wird die mathematische Grundlagenforschung nicht ersetzen.
Wir stehen also am Anfang einer sich abzeichnenden Veränderung in den Forschungsabläufen. Aber eben auch nur an den Abläufen. Eine KI wird die mathematische Grundlagenforschung nicht ersetzen. Im unendlichen Universum aller mathematischen Theoreme suchen wir nach den relevanten, tiefsinnigen, anwendbaren Theoremen. Allerdings sind die allermeisten Theoreme irrelevant oder banal oder weniger spannend als andere.
Das Theorem „7+4=11“ ist eben irrelevant und banal. Und das Theorem „Der Würfel hat 8 Ecken, 12 Kanten und 6 Seitenflächen“ ist weniger spannend als das Theorem „Für beliebige Objekte im dreidimensionalen Raum ohne Löcher mit Ecken, Kanten und Seitenflächen ergibt die Anzahl der Ecken plus Anzahl der Flächen minus Anzahl der Kanten immer 2.“ (Probieren Sie das einmal an den Platonischen Körpern aus! Und falls Ihnen das zu einfach ist, zerlegen Sie die Oberfläche von einem Donut – natürlich nur auf dem Papier – in Drei- oder Vierecke. Dann werden Sie statt 2 immer 0 herausbekommen.) Wenn man eine KI mit den richtigen Daten füttert, kann diese solche Eigenschaften herausfinden.
Aber eine KI wird niemals entscheiden können, ob diese Eigenschaft relevant oder tiefsinnig oder anwendbar ist. Und sie kann auch nicht selbstständig herausfinden, warum diese Eigenschaft universal für alle Objekte gültig ist.
Wissenschaftsmagazin Rubin kostenlos abonnieren